Prof.  Mikhail Sergeyevich  Ermakov
Mechanical Engeneering Problems Institute St.Petersburg 199178,  Russia

Title: On the Limits of the Possibilities in Consistent Nonparametric Statistical Inferences

Abstract:

We discuss necessary and sufficient conditions for existence of consistent procedures in nonparametric estimation and nonparametric hypothesis testing. The same conditions we also explore for the rate of convergence of statistical procedures.

Keywords: uniform consistency, nonparametric estimation, goodness of fit tests, signal detection, rates of convergence.

In approximation theory, ill-posed problems, nonparametric estimation compactness requirement of sets of parameters is necessary condition for reasonable solution of the problem. At the beginning of the talk we discuss the same problem for nonparametric hypothesis testing [1]. For nonparametric signal detection in Gaussian white noise we show that the same compactness assumption is necessary for sets of alternatives if we verify simple hypothesis and sets of alternatives is convex set in L2 with ”small ball” in Lp, p > 1, deleted (radius of ”small balls” tends to zero
with decreasing of power of noise). The same statement has been established for the problem of nonparametric hypothesis testing on a density.
We discuss necessary assumptions for existence of nonparametric estimators having a given rate of convergence and show that belonging to Besov bodies with certain parameters are such assumptions. We find nonparametric estimators having sharp minimax asymptotic on Besov bodies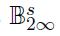  for a certain definition of Besov norm [3]. It turns out that this nonparametric estimator coincide with Bayes estimator of Tikhonov regularization algorithm. Thus one can say : Nonparametric Minimax equals Nonparametric Bayes. We show that traditional sharp asymptotically minimax Pinsker estimator on Sobolev balls [4] has additional logarithmic term in rate of convergence on Besov 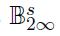bodies.
Distance method is traditional technique for testing nonparametric hypothesis. Thus we describe all distinguishable nonparametric sets of alternatives for test statistics of Kolmogorov, Kramer-von Mises, chi-squared tests with increasing numbers of cells and others [1, 2]. Nonparametric sets of alternatives can be defined both in terms of distribution functions and densities.
[1] Ermakov, M.S. (2020). On uniform consistency of nonparametric tests I. arXiv:2003.05619. .
[2] Ermakov, M.S. (2020). On uniform consistency of nonparametric tests II. arXiv:2004.07039.
[3] Ermakov M.S. (2020) Minimax Nonparametric Estimation on Maxisets. Journal of Mathematical Sciences v. 244, p.779 788.
[4] Johnstone, I. M. (2015). Gaussian estimation: Sequence and wavelet models. New York, NY: Springer.

Biography:

I, Mikhail Sergeyevich Ermakov, was born on 12/25/1952. In December 1975 I graduated from the Faculty of Mathematics and Mechanics of Leningrad State University with a degree in mathematics. Since January 1976 I have been a trainee researcher at the Laboratory of Statistical Methods of the Leningrad Branch of the Mathematical Institute, Academy of Sciences of the USSR. Since January 1978. I am a junior researcher there. In 1979. I defended my PhD thesis. At the Mathematical Institute, I, together with Professors I.A.Ibragimov (POMI) and R.Z.Khasminsky (Institute of Information Transmission Problems of the USSR Academy of Sciences), explored the problem ”when sequential estimation provides a significant gain compared to estimation with a fixed sample size” [1]. This problem was set by academician Yu.V.Linnik.

From September 1981 to September 1992, I worked at the applied institutes of the USSR Academy of Sciences and Leningrad State University. Basically, I was engaged in solving applied problems of probability theory and mathematical statistics. In particular, for solving applied problems in the geophysics in 1990, I received a diploma of a senior researcher in the specialty ”geophysics”. 

At the same time, I continued my research on mathematical statistics. I have constructed asymptotically minimax estimators in the deconvolution problem with Gaussian stationary noise [2, 3], if a priori information is given that solution belongs to a ball in Sobolev space. I found asymptotically minimax tests for the problem of detecting a signal in Gaussian white noise when the set of alternatives is an ellipsoid in L2 with a cut-out ”small ball”[4]. These results are obtained for the strong asymptotics of the convergence rate of L2-norms of estimators and probabilities of type I and type II errors, respectively. 

In 1992 I defended my doctoral dissertation in probability theory and mathematical statistics in St.Peterburg Branch of the Mathematical Institute, Academy of Sciences. The research has been devoted asymptotic problems of statistics.

From September 1992 to the present I have been working a leading researcher at the Laboratory of Reliability Theory Methods at the Institute for Problems in Mechanical Engineering of the Russian Academy of Sciences. Below main scientific results for subsequent years are provided. 

1. Extension to the zone of moderate deviation probabilities of Hajek-Le Cam lower bound in statistical estimation. Similar results were obtained for Pitman efficiency in hypothesis testing. These results were obtained for both strong and logarithmic asymptotics [5, 6]. 

2. Proof of the asymptotic minimax properties of classical nonparametric tests when the set of alternatives are provided in terms of the distance method [7, 8] 

3. The necessary and sufficient conditions were established for the uniform consistency of sets of hypothesis and alternatives for the most widespread setups of hypothesis testing (hypothesis testing on a density, intensity of Poisson process, signal detection, ill-posed problems with Gaussian noise and so on) [9, 10]. Here we supposed that the sets of hypotheses and alternatives are consistent if there is tests for which they are consistent. 

4. The necessary and sufficient conditions for the uniform consistency of sets of alternatives are established for the most widespread nonparametric tests. Conditions were provided for sets of alternatives defined both in terms of distribution functions and densities [8]. 

From September 1996 to the present I have been a professor at the Department of Statistical Modeling of the Faculty of Mathematics and Mechanics of St. Petersburg State University. I lecture on intermediate and advanced statistics for bachelors, masters and postgraduate students.