Prof. Sergey I. Martynenko
Federal Research Center of Problems of Chemical Physics and Medicinal Chemistry of the Russian Academy of Sciences, Russia
Title: A New Approach to Mathematical Modeling of Fluid Dynamics and Heat Transfer
Abstract:
The main trends in modern mathematical modeling are
construction of more accurate submodels of the individual physical and chemical
processes and development of black-box software for solving the industrial
problems (multiphysics simulation). For
black-box software, it is necessary to construct the mathematical models with
the least number of assumptions and the computational algorithms with the least
number of problem-dependent components for numerical solution of the
(initial-)boundary value problems [1].
The
mathematical description of liquid or gas motion is based on the continuum
approximation at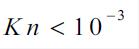 
[2]. The continuum is a hypothetical continuous medium
that is similar to real liquid or gas in macro scale. Any part of continuum is
continuum. Traditionally, the
fluid dynamics equations are obtained based on the conservation laws (mass,
pulse, energy and others) and phenomenological laws (Newton’s law of viscosity,
Fourier's law of heat transfer and others) for an
arbitrary finite volume in a flow. Reduction of the finite volume to
point leads to the Navier-Stokes equations. In this case, all macroparameters
(density, pressure, temperature and others) lose their physical meaning (
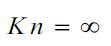). In addition, all functions must be sufficiently
differentiable. Leonhard Euler used differential
and integral calculus to solve these governing differential equations in
engineering applications.
To
overcome the above mentioned physical difficulties, it is proposed to reduce
the finite volumes only until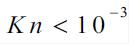 
This makes it
possible to describe the motion of liquids or gases without partial derivatives
and additional requirements for the smoothness of functions. It is shown that
all functions are constant inside the finite volumes and discontinuous on its
faces. The discontinuities of the solutions of the governing equations define
the discontinuous approximation to mathematical description of liquid or gas
motion. The governing equations for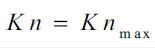 
are exact, and
the classical (differential) Navier-Stokes equations are approximate, where 
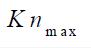is the maximum
permissible Knudsen number for the given problem at which the molecular
structure of matter can be ignored. The discontinuous (derivatives-free)
descriptions of the liquids or gases motion are not only more physically
justified, but also more convenient for computer simulation: the governing
equations and their discrete analogue coincide for the diffusion problems and
are close for the convective-diffusion problems.
The
absence of partial derivatives significantly simplifies numerical solution of
the governing equations; this allows one to avoid using the finite element
method, the finite difference method, high-order difference schemes and other
numerical methods for solving (initial-)boundary value problems. In addition,
the proposed approach fits well with the agglomeration-based multigrid methods
[3].
Thus, the
proposed discontinuous approach to describing the liquid and gas motion will
not only allow us to avoid assumptions of physical nature, but also to combine
the discretization of the governing equations and effective multigrid method
for their parallel solution into unified computing technology for black-box
software.
Acknowledgments
The work is funded by Russian Foundation
for Basic Research (project «Development
and application of high-performance parallel algorithms for supercomputer
modeling of complex reaction flows», project code 21-51-46007) and Scientific
and Technological Research Council of Türkiye (TÜBİTAK), Grant №:
ARDEB-220N170.
References
1. Martynenko S. I. Numerical Methods for
Black-Box Software in Computational Continuum
Mechanics: Parallel High-Performance Computing. Berlin: De Gruyter, 2023, 136
p.
https://doi.org/10.1515/9783111319568
2. Xu K. Direct modeling for computational
fluid dynamics. Acta Mechanica Sinica. V.31, 2015. pp. 303–318.
https://doi.org/10.1007/s10409-015-0453-2
3. Martynenko S. I. Modeling of heat and
mass transfer in the discontinuum approximation,
Vestnik Udmurtskogo Universiteta.
Matematika. Mekhanika. Komp’yuternye Nauki, 2024 (in Russian, in print)
Biography: