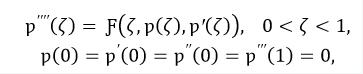
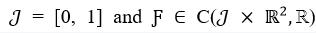
with , with the derivatives holding significant physical interpretations and the system is subjected to certain assumptions. This work introduces a novel methodology for addressing the boundary value problem by utilizing coupled fixed point theory within the GV-FMS framework, characterized by an H-type t-norm. The presentation will be divided into two key segments. The first segment will detail the establishment of the existence and uniqueness of coupled fixed points for mixed monotone mappings under nonlinear contraction within ordered GV-FMS, structured by an H-type t-norm. To validate these theoretical findings, MATLAB (R2022b) is employed for experimental verification, providing both graphical and computational insights. The second segment will explore the application of these results, culminating in the derivation of a unique solution to the cantilever beam problem, highlighting the practical significance and broader implications of this research. 

This talk will shed light on innovative approaches to a classical problem, demonstrating the intersection of mathematical theory and practical application, and is expected to resonate with both theorists and practitioners in the field. 

Key Words: Partially ordered set; GV-FMS; H-type t-norm; Coupled common fixed point; Cantilever Beam Problem. 

AMS Classifications: 47H10, 54H25. 

I am a doctoral degree holder and completed my research Ph.D. degree from one of the most renowned institutions “JC Bose University of Science & Technology, YMCA Faridabad, India”. I secured 13th ranking at All India level in CSIR-NET examination conducted by Council of Scientific and Industrial Research, which is the fundamental examination for the post of assistant professorship and fellowship to carry research in India. Recently, I had been awarded the “Best Researcher Award” in National Faculty Award 2023-24 by Novel Research Academy, Puducherry, India. 

My specialization of research is Fixed Point Theory and Applications. The theory itself is a blend of pure and applied mathematics and has three main streams: 

1. Topological Fixed Point Theory; 2. Metrical Fixed Theory; 3.  Discrete Fixed Point Theory. 

Among these, my area of research is Metrical Fixed Point Theory, which indeed, is a robust field of research in modern times. 

Mathematically, the intersection of the curve described by y = ћ(ϰ) with the line y = ϰ yields the fixed point of the curve y = ћ(ϰ). Specifically, solving the equation ћ(ϰ) = ϰ provides the fixed point for the self-mapping function ћ, which is defined on the abstract set Ӽ. A point ɑ ∈ Ӽ is considered a fixed point of the mapping ћ if it remains invariant under the action of ћ, meaning that ћ(ɑ) = ɑ. 

This concept of fixed points, central to the field of mathematics, is a cornerstone of fixed point theory. This theory combines elements of topology, analysis, and geometry and has been a powerful tool for studying nonlinear phenomena over the past five decades. Its applications extend to a wide range of disciplines, including physics, chemistry, biology, engineering, economics, and game theory. 

Fixed point theory has consistently captivated the interest of researchers. Its applicability is not limited to metric spaces but extends to various spaces, such as partial metric spaces, Ԍ-metric spaces, Menger PϺSpaces, PԌϺ-Spaces, and fuzzy metric spaces. Recently, the theory has gained attention in spaces equipped with a partial order. Moreover, a specialized branch of this theory, known as "coupled fixed point theory" has become a subject of active exploration by researchers. The branch of fixed point theory where no selfmappings are being considered rather the mappings under consideration have the domain as the product space Ӽ   Ӽ and co-domain being the space Ӽ. 

Often problematic situation arises in realistic world where it is not possible to talk about the comprehensive truthfulness or falsity of the solution but intermediate explications are required. In such circumstances fuzzy theory play its vital role addressing all the required affirmations. The theory itself is based on the flexibility of membership that lie in between complete falseness (0) and trueness (1). On the other hand, the notion of metric (distance) has a pivotal application in real world scenario. Fuzzification of metric and hence, of metric spaces provides a mathematical path to deal with the problematic conditions emerging in different diverse fields including engineering and physical sciences. Consequently, the thrust area that has attracted the attention of researchers now-a-days is the application of fixed point theory in fuzzy metric spaces.